And the argument of that paper was that using machine learning we can do that mapping much better because a) the learned model (in this case neuronal network) is much smaller than a traditional b-tree, and b) the learned model can predict the CDF value much more accurately than a simple b-tree, which improves performance.
Now I am all in favor of trying out new ideas, and adapting to the data distribution is clearly a good idea, but do we really need a neural network for that? Because, after all, the neuronal network is just an approximation of the CDF function. There are many other ways to approximate a function, for example spline interpolation: We define a few knots of the spline, and then interpolate between the knots. For example (picture by D.J. Graham)
Thus, what we need for a spline are a sequence of knots where we can interpolate between, i.e., a sequence of (x,y) values.
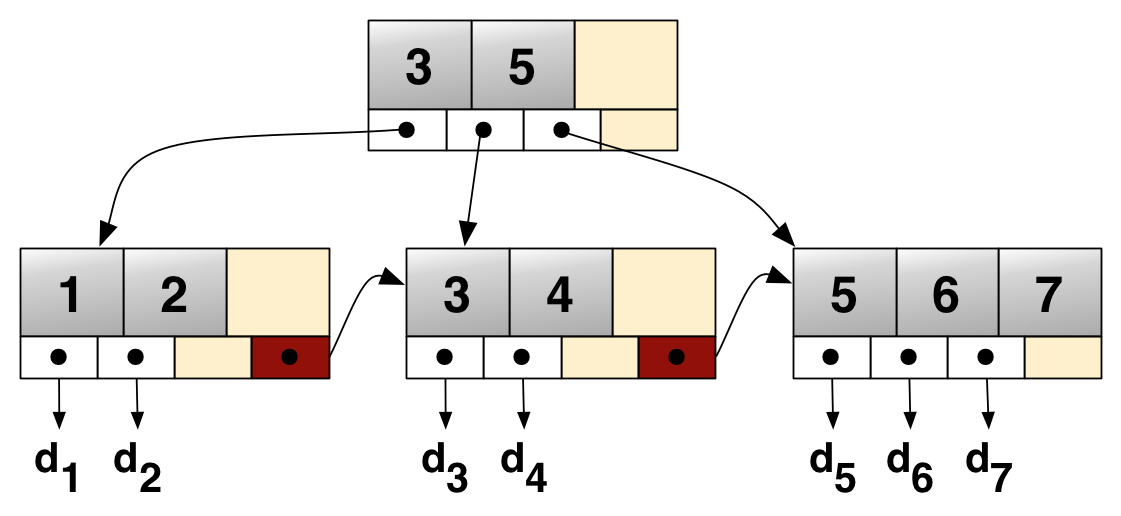
Now, if we think back about traditional index structures, in particular B-trees, we see that they have something similar:
The inner pages consist of separator values, and offsets to the next lower level. Well, we can interpret that as a spline. Instead of just going down to the next level and then doing binary search in the next node, we can interpret our search key as position between the two separators, and then interpolate the position of our search key one the next level. This estimate will be slightly off, of course, but the same is true for the machine learning approach, and we can use the same binary search strategy starting from our estimated position. We can use that interpolation strategy on all levels, both when navigating the inner pages and then going down to the leaf nodes.
How well does that work in practice? The learned indexes paper gives accuracy results and performance results for different sizes of neuronal network models. In the paper the b-trees are depicted as being very large, but in reality that is a parameter, of course. We can get arbitrarily sized b-trees by modifying the page size of the b-tree. For comparisons we chose the b-trees to have the same size (in KB) as the neuronal networks reported in the paper. The source code of the learned indexes approach is not available, thus we only report the original numbers for the neuronal networks. Our own proof of concept code is available upon request. As data sets we used the map set and the lognormal set mentioned in the paper, as we could not obtain the other data sets.
If we just look at the accuracy of the prediction of the final tuple we get as average error the number shown below. For the b-trees we report distance between the estimated position and the real tuple position, averaged over all elements in the data set. For the neuronal networks the wording in the paper is a bit unclear, we think the numbers are the average of the average errors of the second level models, which might be slightly different.
| Map data | size (MB) | avg error |
| Learned Index (10,000) | 0.15 | 8 ± 45 |
| Learned Index (100,000) | 1.53 | 2 ± 36 |
| Complex Learned Index | 1.53 | 2 ± 30 |
| B-tree (10,000) | 0.15 | 225 |
| B-tree (100,000) | 1.53 | 22 |
| Log normal data | size (MB) | avg error |
| Learned Index (10,000) | 0.15 | 17,060 ± 61,072 |
| Learned Index (100,000) | 1.53 | 17,005 ± 60,959 |
| Complex Learned Index | 1.53 | 8 ± 33 |
| B-tree (10,000) | 0.15 | 1,330 |
| B-tree (100,000) | 1.53 | 3 |
If we look at the numbers, the interpolating b-tree doesn't perform that bad. For the map data the learned index is a bit more accurate, but the difference is small. For the log normal data the interpolating b-tree is in fact much more accurate than the learned index, being able to predict the final position very accurately.
What does that mean for index performance? That is a complicated topic, as we do not have the source code of the learned index and we do not even know precisely on which hardware the experiments were run. We thus only give some indicative numbers, being fully aware that we might be comparing apples with oranges due to various differences in hardware and implementation. If we compare the reported numbers from the paper for lognormal with our proof of
concept implementation (running on a i7-5820K @ 3.30GHz, searching for every element in the data set in shuffled order) we get
| Log normal data | Total (ns) | Model (ns) | Search (ns) |
| Learned Index (10,000) | 178 | 26 | 152 |
| Learned Index (100,000) | 152 | 36 | 127 |
| Complex Learned Index | 178 | 110 | 67 |
| B-tree (10,000) | 156 | 101 | 54 |
| B-tree (100,000) | 171 | 159 | 12 |
Again, the b-tree does not perform that bad, being virtually identical to the reported learned index performance (remember the caveat about hardware differences!). And the b-tree is a very well understood data structure, well tested, with efficient update support etc., while the machine learning model will have great difficulties if the data is updated later on. Thus, I would argue that traditional index structures, in particular b-trees, are still the method of choice, and will probably remain so in the foreseeable future.
Does this mean we should not consider machine learning for indexing? No, we should consider everything that helps. It is just that "everything that helps" does not just include fashionable trends like machine learning, but also efficient implementations of well known data structures.

Why do I get a feeling this is the modern version of John Henry? Instead of man against machine, we have the old machines competing against the new AIs.
ReplyDeleteI don't think that is the right analogy for learned indexes. There is a reason why this is called machine learning and not artificially intelligence. There is no intelligence involved here at all, this is "just" learning the cumulative distribution function.
DeleteWhich still a hard problem, but not AI level hard. Function approximation is a well studied field, and we know many different approaches to that. The only question is what is the best approach, considering dimensions like accuracy, performance, and updateability.
Hi Thomas,
ReplyDeleteGreat to see your interest in learned indexes. Yet, we would like to clarify a few things:
- Why not use other models than NN: We could not agree more. The main point of the paper is to offer a new view on how to design data structures and algorithms, and we make the case that machine learning can help. We just use neural nets because of their generality and potential for TPUs. At the same time, many other types of models can work and might be better. Ideally, the system would try automatically different types of models from B-Trees to splines to neural nets. It just always depends on the use case what works best. For example in the log-normal data set, the log-normal CDF function would probably be the smallest and fastest index structure available.
- Performance results: we tried your described approach in one of the first iterations and it had comparable performance to our B-Tree implementation. In fact, there is another paper under submission from Brown, which studies how the leaf nodes of a BTree can be merged using linear functions. However, we did find that the search between the layers of the BTree (even with interpolation search) has a negative impact of the performance. In our experiments your described technique was roughly 2x slower than the best learned indexes.
The best indicator that it is an apples-to-oranges comparison can be seen in your B-Tree(10,000) case vs our B-Tree implementation. The avg. error for your B-Tree(10k) case is 225 but the search takes only 54ns. In contrast, our most fine-grained B-Tree with an average error of 4 takes 52ns to find the data. With an average error of 128 (page size 512) it takes 154ns in our paper, so 3x longer than your implementation while still having a smaller average error (I make the assumption here, that the average error between B-Trees is actually comparable.)
There might be several factors contributing to it:
(1) The hardware as you already pointed out.
(2) The record size. We always used records with a key and a payload and we already know that the payload can have a significant impact.
(3) Our general learned index framework and other implementation details.
In addition, it would be interesting to know how the performance numbers for the map data looks like. Our guess is, that they are worse than the log-normal performance numbers given the higher error. At the same time we report even better numbers for them (under 100ns)
- On Inserts: You statement that "machine learning model will have great difficulties if the data is updated later on" is not so clear to us. In fact, if the new data follows roughly the same trend/distribution of the existing data, even inserts could become faster, ideally O(1). To some degree the rebalancing of a B-Tree is nothing else than retraining a model and there is more and more work on how to provide better guarantees for ML under changing conditions. But clearly more research is needed here to understand this better.
- Your final words that we should try everything that helps including efficient implementations. Yes and double yes! Learned indexes are just another tool and it highly depends on the use case. Our hope is that further research will continue to refine that tool and understand those use cases so that learned indexes are trusted as much as B-Trees.
Best,
Tim, Alex, Alkis, Ed, Jeff
Hi Tim,
Deletethanks for your long comment, I am not sure that I can do it justice, today being Christmas Eve and my kids pulling me around. Just a few short comments:
For updates, your idea of leaving reserve space for new elements works until the reserve space is full. Incidentally the same is true for b-trees, you can insert into a fixed sized b-tree bucket in O(1) if the bucket is not full. But at some point all free space is gone, and then you must pay a price. Which is no surprise, if you could insert n elements in O(n) in a sorted data structure for arbitrary large n, you could sort n element in O(n), which is not possible in the general case. Plus the data distribution might change over time, you may want to support updates and deletions, etc. Which is all well understood for b-trees, but probably difficult for a learned model.
A detail that puzzled me about your experiments is that if you compare Figure 5 and 6, in Figure 5 you get a lookup time of ca. 100ns for an error of 20. In figure 6 you get a lookup time of ca.100ns for an error of 17,000. Do you have an idea what that happens?
Overall your paper is quite interesting and has caused a lot of discussion, which is a good thing! I even discuss it in some of my lectures. I still believe more in b-trees than in machine learning, in particular for the general use case, but I am always interested in new ideas.
Best
Thomas
I suspect at least some of the learned index work is designed specifically for Google's tensor units and their low-accuracy but high-parallelism computations.
ReplyDeleteHi Thomas,
ReplyDeleteno worries! Family always comes first and I am also pretty busy right now with Christmas preparations. Just a "quick" answer to your two questions:
For updates, the difference between BTrees and learned indexes is that the available space is more intelligently spread. This allows for much more O(1) inserts. Plus it can be really O(1), as in the case of the BTree you still need to search the key, which is O(log n). The idea also better separates the processes of inserting and adding space. For example, you could insert space during night for the best performance during the day. But you are right, if the distribution shifts, this is not yet as well-understood and a great future research direction (Alkis and I had plenty of discussions about it).
On the high log-normal error: yes, this is because of a particularity of our training process and the std err alone is not a good indicator here. The reason why we also included the std. err variance between buckets. However, a mean-value or better a per bucket-size-weighted std. err/mean would be more representative; something we can fix in the next revision of the paper. Let me send you more details on it after Christmas when I have time to dig up the numbers.
However note, that with small changes in the model search process, we could (easily) achieve even much better numbers for the log-normal data than for the map-data as it is not hard to learn the often simple distributions of a data generators. We will also expand on this in the next revision of the paper.
Glad to hear, that the paper achieved its main goal to offer a new tool and view on indexing. However, I do see a lot of potential in the idea, especially when combined with clever auto-tuning of the models and the hybrid indexing idea. The hybrid index can take advantage of the distribution where possible and degrades to a BTree where it does not make sense. So even without GPUs/TPUs it should provide significant benefits.
Merry Christmas to you and your family and let's catch up after the holidays,
Tim
Alex Beutel just pointed out to me, that the spacing argument might be misleading. An oversized (very low fill-level) BTree would also space out the available space. However, it does not do it within the page, meaning every insert would still occur a certain cost, especially for large pages, plus of course the cost for finding the page in the first place. The more interesting thing is, that we can use online learning to update our index in a way btrees may not be able to for shifting distributions. Again much more research is needed here to understand that better.
DeleteHi Tim,
DeleteI hope you enjoy the holidays, we will have to continue the discusses afterwards. Just some remarks: In your paper you argue that indexes are models. If we follow that argument, it holds in both directions: Not only can we approximate an index with a model, but we can also interpret an index as a model. This means that each and every trick that you apply to improve update behavior could be applied to b-trees, too, if it made sense to do so. Because it does not really matter if you approximate the CDF with a neuronal network or with a spline. They differ in accuracy, lookup performance, and updateability, but fundamentally they are interchangeable. And we can naturally interpret a b-tree as a spline if we want. (And we know how to update b-trees etc., without additional assumptions about future data distributions).
I am also a bit skeptic about you claims of O(1) lookup in your neuronal network tree. Sure, the cost is fixed if the neuronal network tree is fixed, but a b-tree has O(1) lookup time, too, if you fix the depth of the tree. And the interesting question is if you could live with this 2 level models of yours for arbitrary data sizes. Most likely the answer is no, at some points the errors become so large that you need an additional layer of neuronal networks to keep the estimation errors bounded, and then you are back in the O(log n) world. And that O(1) notations of yours ignores the problem that you have to search the ultimate tuple within the error bounds. To be truly in O(1) you 1) had to limit the absolute error in a hard way, and 2) show that you can get that hard error limit with a fixed sized neuronal network for arbitrary input sizes. Information theory makes me a bit skeptic there. Note that not even hash tables are truly in O(1) if we consider all corner cases, and here we are talking about ordered data structures.
Best
Thomas
Hi Thomas,
DeleteThanks for the detailed comment. You are right that some of the methods for making inserts efficient apply to all types of indexes (B-Trees and learned indexes), but I think there are some details that make learned indexes have some promising opportunities. Let me start with trying to explain the second point about lookup time. The claim of constant time lookups is not for any dataset, but for some datasets. For example, as we discuss in the paper, if our dataset consists of consecutive integer keys, then our model (a linear model with a slope of 1) will take constant time to execute and there is no search time because the error is 0, meaning we have constant time lookups. This of course works for other linear data, even if they are not consecutive integers. Generalizing, the lookup time scales with the complexity of the data (where the time includes how complex of a model is required and how much additional error there is that needs to be addressed through local search). The advantage of the learned index perspective is that ML provides a broad class of models that can match a wide variety of real-world data distributions. This is in contrast to B-Trees for which the lookup time is O(log n) for any data distribution.
As you suggest, blending these perspectives using a short tree with interpolation search may also be sufficient to approximate some functions, but also leads to some clear gaps and inefficiencies. For example, log-normal data has a well-defined continuous CDF, and the challenge going forward is finding more flexible functions to approximate it and other common distributions. As an example of inefficiency, a 2-piecewise linear function for which we have different amounts of data in each piece can be modeled by a small neural network but would not align with the typical branching strategy in a B-Tree.
For inserts, yes learned indexes and B-Trees can leverage many of the same techniques (such as spacing the underlying data), but learned indexes also provide some new avenues for updates. Because B-Trees grow with the size of the data, we need to change the branching structure as the data grows (in addition to shifting around the underlying data). Learned indexes, on the contrary, may not need to actually change as we insert data (the underlying data of course will need to change). That is, if the data comes from the same distribution, the model will still be accurate and no updates to the model are needed. Even if the data distribution changes, the model can update through online learning or simple updates to sufficient statistics (as in linear models). This opens up new opportunities how to adjust an index for data growth and changes in the distribution Again, we find that the cost of updates here corresponds to model (and thus data distribution) complexity and not size of the data. Of course, the paper focuses on lookups not inserts, and we feel there are many open, interesting questions to demonstrate how to best use learned indexes with workloads with many updates/inserts. Overall, for both lookups and inserts, learned indexes offer a broader set of design choices in building index structures.
Thanks,
Alex
Hi Alex,
Deleteyou are right, there is a point in trying out different functions. It is very easy to add linear approximation to b-trees, but linear approximations are not always appropriate. Trying out different schemes, for example using a learning method, is certainly a good idea.
I hope my blog post did not came out too negative, I am not against trying different schemes. I am bit skeptic about the learned index for the general use case, for data is changed over time and where the data distribution is not known a priori (and might even change over time). But if the data is static, like in the read-only use case that Mark has asked about below, than it absolutely makes sense to try to adapt to the data distribution as much as possible.
I am not sure I good your point about evenly distributed integers. If the numbers are nice (e.g., dense or evenly space integers), than the b-tree interpolation would work perfect, too. It would never fall back to binary search and directly jump to the correct position. The only log n at all would be that it does the interpolation once per b-tree level. Which is usually a very small number. And one could try to avoid even that by recognizing that the spline errors are very small, and skip whole b-tree levels. (But admittedly that kind of precomputation makes more sense if the data is largely static, and then one could try even better spline construction algorithms instead of regular b-tree separators, as I have mentioned in my post to Mark).
Best
Thomas
Thanks, Thomas. The post and comments are definitely not negative, and I appreciate the chance to dissect these ideas. I agree that interpolation search seems sufficient for precisely linear data. Rather, I was using linear data as a simple example for which it is clear we can have constant time lookups (in this case for both interpolation search and learned indexes), and to show this can be extended to other cases where the data is not linear but would still precisely match our model. For updates, I agree it is so far not as well understood as B-Trees, but I would also argue that there are no obvious blockers. We will see what we can do.
DeleteI am interested in the topic for read-only index structures like the per-SST block indexes and bloom filters in an LSM. How can space and search efficiency be improved compared to what is currently done for RocksDB. The SILT paper has interesting results on that topic for the SortedStore - https://www.cs.cmu.edu/~dga/papers/silt-sosp2011.pdf
ReplyDeleteIf your data is read only you do not need the update capabilities of b-trees. And in general you can probably afford to spend more time on preprocessing to get a good representation.
DeleteTims machine learning approach for example might be an interesting option, as you do not have to worry about updates. Or you use a classical function approximation approach with hard error bounds, like this one here:
Michael T. Goodrich: Efficient Piecewise-Linear Function Approximation Using the Uniform Metric. Discrete & Computational Geometry 14(4): 445-462 (1995)
or similar approaches. The later ones tend to be a bit math heavy, but they have the advantage that they are provably optimal, they are not heuristics. The can be computed in reasonable time (Goodrichs algorithm runs in O(n log n)), but they cannot be updated. For read only data sets that isn't a problem, of course.
The SILT paper uses compact, but updateable data structures like, e.g., tries. In general that is a good idea, of course. But if you know beforehand that you will never update your data that might be wasteful, and direct approximation of the CDF could be an interesting option.
You point out that not having any code available from the "learned index" paper makes comparison difficult, yet you decided to make your own code available "upon request" only. Both choices make the results harder to reproduce and study, they hamper experimenting with the design space.
ReplyDeleteWell, the code is available, I have already given it out to several parties. But this is a proof-of-concept hack and in no way ready for productive usage. I would therefore like to add usage instructions and clarify issues if needed. If I just provide a download link people report that the code is hard to use and does not work as expected.
DeleteBut I am happy to provide the code to you (with instructions), just drop me a mail.
Hi Thomas,
ReplyDeleteStarted reading the paper some days back.
Sure there is great potential in the idea of replacing the traditional indexes with the machine learning models. But while researching i came across your blog discussions with Tim and Alex, and it is definitely helpful to carry out the future research in software systems direction.
Just a quick question. So it's almost been 2 years since paper has released, is there anything changed in database community due to this paper? and also since you mentioned you had tried out the implementation of the paper. Would it be possible for you to share it across?
Thanks
Vinayak
I am not aware of any system that has implemented learned models. Probably due to the difficulty of construction/updates. If you are interested in the setting there is an upcoming paper (Learning to Search, http://mlforsystems.org/accepted_papers.html) about learned indexes and other alternatives, including spline based approaches. Both source code and data will be available.
DeleteHi Thomas,
ReplyDeleteThank you so much for the information.
Is there any implementation available for "The Case for learned index structure".?
I checked out the "Learning to Search", but it seems unavailable for now in the above mentioned website.
Thanks,
Vinayak
Both paper and code will be available soon. The camera ready deadline is on Friday, so the paper should be online soon-ish. The workshop itself is on December 15th, the code and the benchmark will be released before that.
DeleteNote that this is not the original code from "The Case for learned index structure". But it compares different learned approaches with other alternatives, including the spline idea mentioned in a newer blog post in this blog.
Hi Thomas,
ReplyDeleteThank you for the update, was following up the ML for systems accepted papers page for last few days,but what i saw the topic "learning to search" was removed suddenly yesterday. Is it replaced with "SOSD: A Benchmark for Learned Indexes." and are this both papers same?
Thanks,
Vinayak
yes, that is the same paper. The source code is available at https://github.com/learnedsystems/sosd
DeleteThe reproduce.sh script builds everything to reproduce the experiments.