And the argument of that paper was that using machine learning we can do that mapping much better because a) the learned model (in this case neuronal network) is much smaller than a traditional b-tree, and b) the learned model can predict the CDF value much more accurately than a simple b-tree, which improves performance.
Now I am all in favor of trying out new ideas, and adapting to the data distribution is clearly a good idea, but do we really need a neural network for that? Because, after all, the neuronal network is just an approximation of the CDF function. There are many other ways to approximate a function, for example spline interpolation: We define a few knots of the spline, and then interpolate between the knots. For example (picture by D.J. Graham)
Thus, what we need for a spline are a sequence of knots where we can interpolate between, i.e., a sequence of (x,y) values.
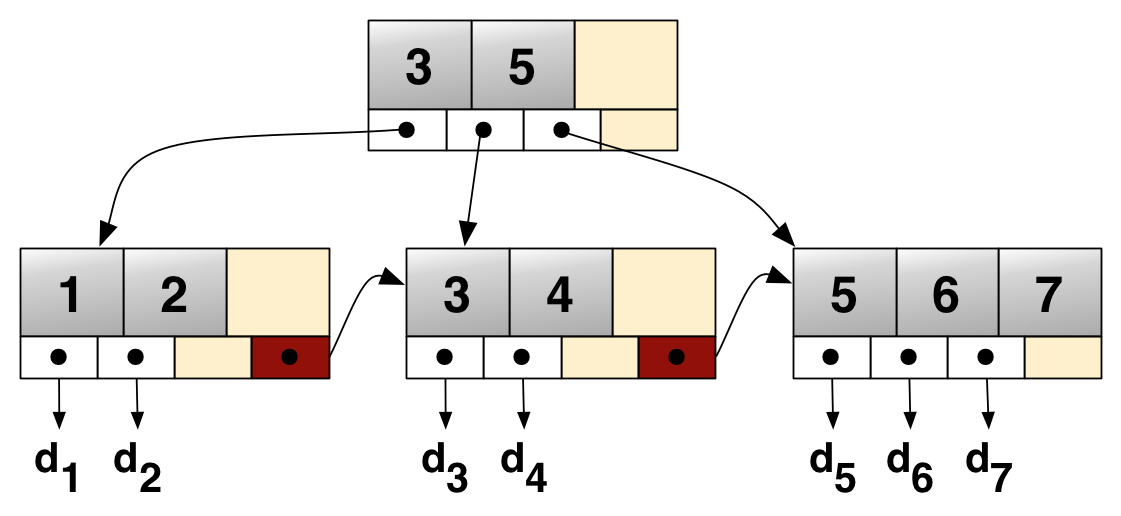
Now, if we think back about traditional index structures, in particular B-trees, we see that they have something similar:
The inner pages consist of separator values, and offsets to the next lower level. Well, we can interpret that as a spline. Instead of just going down to the next level and then doing binary search in the next node, we can interpret our search key as position between the two separators, and then interpolate the position of our search key one the next level. This estimate will be slightly off, of course, but the same is true for the machine learning approach, and we can use the same binary search strategy starting from our estimated position. We can use that interpolation strategy on all levels, both when navigating the inner pages and then going down to the leaf nodes.
How well does that work in practice? The learned indexes paper gives accuracy results and performance results for different sizes of neuronal network models. In the paper the b-trees are depicted as being very large, but in reality that is a parameter, of course. We can get arbitrarily sized b-trees by modifying the page size of the b-tree. For comparisons we chose the b-trees to have the same size (in KB) as the neuronal networks reported in the paper. The source code of the learned indexes approach is not available, thus we only report the original numbers for the neuronal networks. Our own proof of concept code is available upon request. As data sets we used the map set and the lognormal set mentioned in the paper, as we could not obtain the other data sets.
If we just look at the accuracy of the prediction of the final tuple we get as average error the number shown below. For the b-trees we report distance between the estimated position and the real tuple position, averaged over all elements in the data set. For the neuronal networks the wording in the paper is a bit unclear, we think the numbers are the average of the average errors of the second level models, which might be slightly different.
| Map data | size (MB) | avg error |
| Learned Index (10,000) | 0.15 | 8 ± 45 |
| Learned Index (100,000) | 1.53 | 2 ± 36 |
| Complex Learned Index | 1.53 | 2 ± 30 |
| B-tree (10,000) | 0.15 | 225 |
| B-tree (100,000) | 1.53 | 22 |
| Log normal data | size (MB) | avg error |
| Learned Index (10,000) | 0.15 | 17,060 ± 61,072 |
| Learned Index (100,000) | 1.53 | 17,005 ± 60,959 |
| Complex Learned Index | 1.53 | 8 ± 33 |
| B-tree (10,000) | 0.15 | 1,330 |
| B-tree (100,000) | 1.53 | 3 |
If we look at the numbers, the interpolating b-tree doesn't perform that bad. For the map data the learned index is a bit more accurate, but the difference is small. For the log normal data the interpolating b-tree is in fact much more accurate than the learned index, being able to predict the final position very accurately.
What does that mean for index performance? That is a complicated topic, as we do not have the source code of the learned index and we do not even know precisely on which hardware the experiments were run. We thus only give some indicative numbers, being fully aware that we might be comparing apples with oranges due to various differences in hardware and implementation. If we compare the reported numbers from the paper for lognormal with our proof of
concept implementation (running on a i7-5820K @ 3.30GHz, searching for every element in the data set in shuffled order) we get
| Log normal data | Total (ns) | Model (ns) | Search (ns) |
| Learned Index (10,000) | 178 | 26 | 152 |
| Learned Index (100,000) | 152 | 36 | 127 |
| Complex Learned Index | 178 | 110 | 67 |
| B-tree (10,000) | 156 | 101 | 54 |
| B-tree (100,000) | 171 | 159 | 12 |
Again, the b-tree does not perform that bad, being virtually identical to the reported learned index performance (remember the caveat about hardware differences!). And the b-tree is a very well understood data structure, well tested, with efficient update support etc., while the machine learning model will have great difficulties if the data is updated later on. Thus, I would argue that traditional index structures, in particular b-trees, are still the method of choice, and will probably remain so in the foreseeable future.
Does this mean we should not consider machine learning for indexing? No, we should consider everything that helps. It is just that "everything that helps" does not just include fashionable trends like machine learning, but also efficient implementations of well known data structures.